Jugando con diagramas de árbol

Hace unos días disfruté del placer de abrir un armario de la Facultad y encontrar muchísimos juegos para trabajar las matemáticas.
Os los voy a ir enseñando poco a poco, comienzo con un juego basado en los diagramas de árbol.

El juego consiste en unos tableros con diagramas y distintas imágenes, colores, tanto con elementos clasificatorios o no clasificatorios, es decir, nos permite el trabajo con simbología negativa. Y varios juegos de tarjetas que se colocarán al final de las ramas de acuerdo a la simbología que se indique.

Pero ¿qué es un diagrama de árbol? Es una representación gráfica que recoge todos los resultados de un experimento, de hecho, yo siempre los había utilizado para trabajar con la probabilidad, y en los últimos años para introducir la multiplicación.

Puedes construir el árbol iniciando de un tronco común, y sacando distintas ramas para cada una de las posibilidades que queremos recoger. Podemos ir dividiendo las ramas en otras más pequeñas a través de nudos que van conduciendo las distintas posibilidades.

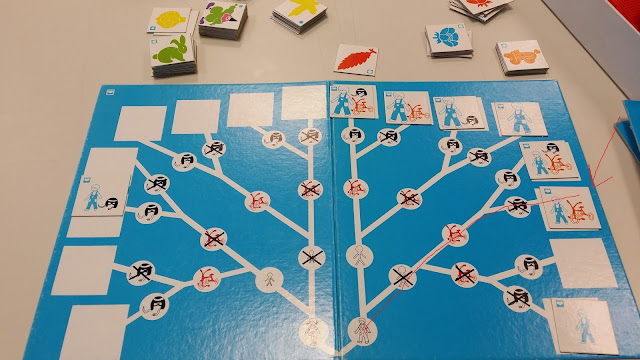
Vamos a fijarnos en la imagen en la que hemos dibujado uno de los recorridos con una línea roja.

El recorrido indica "niño+no grande+con triciclo+sin casco".

De esta forma la persona que juega ha de tomar decisiones en cada uno de los nudos de las ramas del árbol.

De esta manera el niño va siguiendo la trayectoria que nosotros marcamos hasta completar el final. Pero, ¿y si le damos el final y dejamos que ellos coloquen las decisiones en cada uno de los nudos?

Taparíamos algunas de las imágenes en los círculos para que los niños pudiesen elegir qué colocar.

Pero ¿esta es la única forma de utilizar el diagrama de árbol con los niños? Pues no... vamos ver otra posibilidad.

En la imagen vemos cómo los niños han construido un árbol a partir de los bloques lógicos que pueden ir extrayendo de una bolsa opaca.

Fuente: http://www.minedu.gob.pe/soporte-pedagogico/pdf/recursos/matematica/3g_Sesion2_mate.pdf

Y si lo planteas con posibles menús que elaborar, o distintas formas de vestirse.

Fuente: http://lasmatesdemama.blogspot.com.es/2016/11/combinaciones-vestirse-aprendiendo.html

3 ropas x 3 sombreros, ¿cuántas maneras tenemos de vestir a la niña?

Te dejamos que diseñes tus árboles y tus juegos, seguro que puedes contarnos después otras posibilidades.

Referencias bibliográficas:

Antequera Guerra, A.T. & Espinel Febles, M.C. (2011). Resolución de juegos cotidianos con árboles de decisión: aportaciones de una experiencia con alumnos de secundaria. Educación matemática, 23(2), 33-63. Recuperado en 21 de marzo de 2018, de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-58262011000200003&lng=es&tlng=es

Cañadas, M. C. & Figueiras, L. (2009). Razonamiento en la transición de las estrategias manipulativas a la generalización. In Investigación en educación matemática XIII (pp. 161-172). Sociedad Española de Investigación en Educación Matemática, SEIEM. https://dialnet.unirioja.es/descarga/articulo/3628675.pdf

Ruesga, P., Giménez, J., & Orozco, M. (2005). Diagramas de relaciones lógicas en tareas de transformación para preescolares. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 23(3), 403-418. Recuperado en 21 de marzo de 2018, de http://www.raco.cat/index.php/Ensenanza/article/download/22036/332780