La entrada de hoy parte de la lectura de un artículo de investigación, y me gustaría aportar algunas ideas para trabajar estos dos conceptos en el aula a partir de la lectura. El artículo incluye una serie de estrategias para trabajar en el aula, pensando en estudiantes con discapacidad, pero creo que puede ser válida en cualquier diseño de situaciones de aprendizaje con cualquier alumnado. Valoro este tipo de artículos científicos especialmente, por la sencillez de cómo trata la información y por la utilidad que puede suponer en las aulas de la escuela.
Inicio dando la referencia completa del artículo, por si alguien quiere consultarlo (no es en abierto). Utilizaré algunas expresiones literales (y traducidas) tomadas del citado artículo y que incluiré entre comillas.
King, S., Rojo, M., & Bryant, D. P. (2023). Demystifying Area and Perimeter: A Practitioner’s Guide to Strategies That Work. Intervention in School and Clinic, 58(4), 241-248. https://doi.org/10.1177/10534512221093780
Estos dos conceptos me han sorprendido en algunas aulas, desde la perspectiva de las unidades de medida en distintas ocasiones, cuando algunos estudiantes intentaban pasar de unas unidades de longitud a otras de superficie sin plantearse nada más allá de un cálculo, podríamos decir imposible, quizá influidos por haber sido "tratados" con las "
escaleras" como recurso didáctico. Y es que "muchos estudiantes carecen de una comprensión suficiente del área y el perímetro, lo que resulta en el desarrollo de conceptos erróneos que con el tiempo impactan negativamente en su rendimiento en matemáticas".
La estrategia 1 es el uso de recursos manipulativos, buscando que el aprendiz relacione el concepto con la representación. "Los manipulativos se utilizan en
el aula de matemáticas para representar una idea o un proceso de forma concreta y
pueden tener beneficios para el aprendizaje de los estudiantes (Bouck & Park, 2018)". El orden de trabajo en este caso es importante, y me parece adecuado "los estudiantes primero aprenden un concepto matemático con manipulativos concretos, luego aprenden a dibujar una representación bidimensional y, finalmente, resuelven usando solo números y símbolos abstractos".
Uno de los materiales que puede ayudarnos en el aula es el Geoplano, donde iniciaríamos definiendo la unidad de longitud como la distancia entre dos clavijas. El perímetro lo expresaríamos "como la longitud alrededor de una forma", tras lo que facilitaríamos una cantidad y pediríamos a los estudiantes que representasen como perímetro. "Un error común que cometen los estudiantes (...) es contar las clavijas en lugar de los espacios", algo que puede solventarse con una mediación adecuada del docente desde la observación de la forma construida.
Dada que la descrita en el artículo tiene algún aspecto que creo es demasiado procedimental, me atrevo a proponer una secuencia a partir de la construcción de un rectángulo.

Ante el rectángulo podríamos contar cuántos pedazos de goma (segmentos) tenemos en cada uno de los lados, u observar primero la figura plana que tenemos observando sus propiedades, sus lados iguales dos a dos, o la cantidad de pequeños cuadrados que pueden "ocupar" su interior. También resultaría distintos, pensemos aquí trabajar con este material únicamente, el geoplano y sus gomas, o trabajar con pequeños cuadrados que nos llevarían a visualizar la figura plana de manera distinta, una desde la longitud exterior y otra desde el área interior.
"Las cuadrículas son excelentes herramientas para enseñar medidas geométricas porque las unidades se delinean antes de colocar formas sobre ellas y, por lo tanto, actúan como “reglas de área” (Van de Walle et al., 2019)", así podríamos pensar utilizar el geoplano y servirnos de apoyo con pequeños cuadrados que colocar en el interior, que nos facilitarán el conteo y nos permitirán expresar el resultado en forma de "unidades cuadradas". Deducir desde esta observación cómo calcular perímetro y área, tras ver el significado diferencial de ambas puede ser un inicio a la posterior generalización de la fórmula.
La segunda estrategia es centrarse en la variable. "Por ejemplo, cuando se les presentan dos formas que tienen perímetros congruentes y áreas incongruentes, los estudiantes pueden responder que los perímetros de las formas son incongruentes porque la distracción visual de las áreas incongruentes interfiere con el razonamiento de los estudiantes. Sin embargo, llamar la atención sobre la variable de interés reduce el efecto de la interferencia de variables irrelevantes en el pensamiento de los estudiantes (Babai et al., 2016)". La variable de interés en este caso es el perímetro.
El juego aquí podría ser pedir a los estudiantes dibujar formas con el mismo perímetro que den lugar a distintas áreas, por ejemplo utilizando algo tan sencillo como una hoja de papel cuadriculado. Esta situación "puede utilizarse en el aula para disipar la idea errónea de que los perímetros incongruentes siempre deben tener áreas incongruentes y viceversa".
El ejemplo que se sugiere parte de mediar para que el aprendiz pueda discernir y centrarse en la variable. "Primero, comience creando un rectángulo de dos unidades por cuatro unidades con unidades cuadradas individuales hechas de cartulina (es decir, dos cuadrados en cada una de las cuatro filas formarían un rectángulo de 2 × 4 dimensiones). Modele cómo calcular el área contando las unidades cuadradas dentro de la forma".
El siguiente paso buscaría rodear la forma con pequeños trozos de algún material recto, pajitas, trozos de varillas de madera, de la misma longitud (lado de los cuadrados interiores), y que nos facilitasen el conteo de las mismas una vez rodeada la forma. Contemos cuántas tenemos entonces. Primera pareja, una forma: un área y un perímetro. Tomando de nuevo las unidades cuadradas que teníamos (8), formaríamos una forma distinta. En esta situación con el mismo área, al colocar las pequeñas unidades de longitud sobre el borde, es bastante probable que no tengamos suficientes. ¿Por qué?
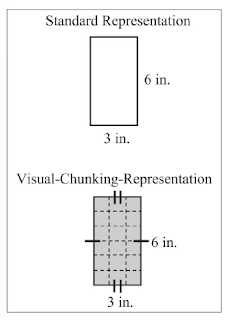
La tercera estrategia busca la fragmentación visual. Para entender a qué nos estamos refiriendo vamos a ver una imagen:
"Un problema de área se representa de dos maneras diferentes: (a) usando la representación estándar y (b) usando VCR. Observe la comparación entre el formato estándar y el VCR. La
representación estándar proporciona a los estudiantes lo siguiente: (a) la forma de la figura, que debería indicarles qué fórmula utilizar; (b) longitud de un lado; y (c) un ancho. Sin embargo, no indica explícitamente que longitudes y anchos opuestos sean equivalentes, lo cual es un
conocimiento previo necesario para resolver el problema. Utilizando la representación estándar, los estudiantes deben retener al menos cinco datos: (a) el tipo de forma, (b) los atributos de la forma, (c) la longitud dada, (d) el ancho dado y (e) los datos relevantes. conocimiento para
determinar la fórmula adecuada a utilizar. Por el contrario, el VCR utiliza fragmentos visuales para indicar a los estudiantes las características visuales importantes dentro de la representación. El acto de fragmentar hace que sea visualmente evidente para los estudiantes que hay tres
grupos de seis unidades dentro del rectángulo al sombrear y dividir el rectángulo en unidades cuadradas individuales. Además, el largo y el ancho están etiquetados con números y unidades correspondientes, junto con una marca en los lados claramente marcada".
Y por último, la cuarta estrategia, la instrucción contextualizada. "Los docentes pueden brindar oportunidades para una instrucción contextualizada en una multitud de formas creativas que aumentan la motivación para completar las tareas y conducen a un mayor mantenimiento y generalización de las habilidades con el tiempo (Collins et al., 2011; Van de Walle et al., 2019). Se puede utilizar de manera efectiva a lo largo de la progresión de la lección y en todos los niveles de grado". Es decir podemos dar un contexto problema que nos conduzca a una práctica donde es necesario interpretar una situación, modelizarla y realizar las correspondientes observaciones y cálculos a partir de ellas. Haciendo que el docente facilite ya inicialmente una representación icónica de la figura o no.
¿Qué opinión tienes de estas estrategias? ¿Puedes aportar otras?