"Consul, el mono culto" un campeón de la multiplicación

Esta mañana se celebró #matesenlacalle, una actividad en que la Sociedad Madrileña de Profesores de Matemáticas "Emma Castellnuovo" saca la parte más rica del aprendizaje matemático a la calle. Hoy ha sido una jornada fría si nos referimos a lo meteorológico pero calentita desde la cantidad de familias que han participado.

Entre estas mesas y gracias a Mar y Dolores, he conocido a Consul, el mono culto (Consul, the educated monkey), ¿os lo presento?

Nuestra actividad era un tablero del 100, los niños tenían tres dados. Los tiraban y elegían dos para multiplicar, y el tercero podían sumarlo o restarlo a la cantidad anterior. 

Ese resultado lo buscaban en el tablero, le dábamos la vuelta y aparecía una palabra o un comodín. El objetivo era completar "MATES EN LA CALLE", en cuatro tiradas.

Fuente de la imagen: Wikipedia

Los dados no han sido dados cúbicos, sino que hemos aprovechado un juego como el que aparece en la imagen para garantizar la posibilidad de obtener números en todo el tablero. 

Pero, ¿dónde aparece Consul en esta actividad? Pues como vemos el objetivo de la actividad es el cálculo mental, unido a la decisión de cómo combinar los números para hacer la operación y que el resultado no estuviese ya destapado, pero por nuestra mesa pasaban niños y niñas de todas las edades, unos con más seguridad que otros en la tarea de multiplicar, y entonces ¿por qué no brindarles una ayuda con cierto toque de magia?

Entonces, aparece nuestro mono, colocamos sus pies sobre los números de los dos multiplicadores y... ¡aparece el resultado en sus manos!

Como vemos en la imagen anterior, los dados nos facilitan el 2 y 3, y el mono dice "6". Si bien es cierto, que no ahondamos en el significado de la multiplicación, sino solo en el resultado, más o menos como la calculadora, pero en el contexto en que estábamos de un día de juego y diversión, nuestro mono sabio nos ha aportado un recurso que ha gustado a grandes y pequeños.

Pero vamos a hablar un poco de este juguete que no es nada moderno, y eso lo veíamos ya desde ver que está fabricado con hojalata y hoy día es difícil encontrar este tipo de material en los juguetes.

Se trata de una curiosa calculadora mecánica que es una réplica de un juguete de hojalata original norteamericano de 1908. La historia nos dice que,

un mono artista llamado Cónsul, adiestrado en Gran Bretaña, llegó a Estados Unidos en 1909. Al parecer, no fue el primer mono adiestrado en recibir el nombre de Cónsul, pero sí el que recibió mayor publicidad. Actuó en espectáculos de vodevil por todo el país (...) en 1915, William Henry Robertson, dibujante de NCR, solicitó dos patentes. La primera, para un dispositivo de cálculo, buscaba un método rápido y sencillo para obtener resultados en una tabla. La segunda, para un juguete que utilizaba el mismo mecanismo para estimular el interés de los niños por el estudio de los números. En esta segunda patente, el mecanismo adoptaba la forma de un mono.

Fuente: https://americanhistory.si.edu/explore/stories/consul-educated-monkey-or-inventions-william-h-robertson

Los entresijos del mecanismo son

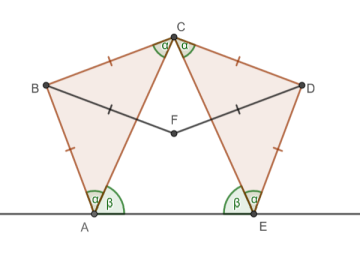
Cada pierna forma una sola pieza con el brazo superior del mismo lado. Tiene tres puntos de pivote: en el pie, en la pajarita y en el codo. Las piezas del antebrazo están conectadas entre sí y a los pivotes del codo. Un aspecto importante es que las distancias desde el codo hasta los demás pivotes son todas iguales. En el diagrama a continuación, esto significa que BA, BC y BF tienen la misma longitud, al igual que DE, DC y DF en el otro lado.

Ignoraré la barra deslizante vertical que sólo sirve para proporcionar una ventana consistente hacia la mesa y para mantener la cabeza del Cónsul erguida.

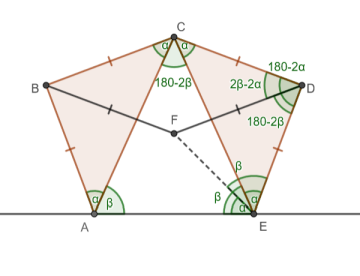
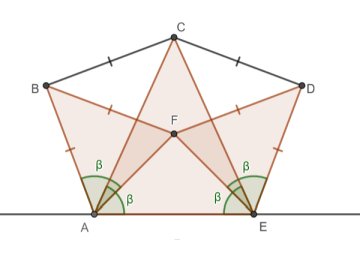
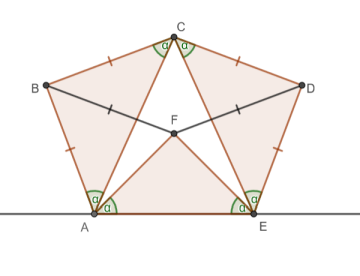
Los ángulos marcados con α (BAC, ACB, CED y DCE) son constantes, pero los ángulos marcados con β (CAE y AEC) varían según la ubicación de los pies del Cónsul. Utilizando triángulos isósceles y el rombo BFDC, se puede trazar un círculo alrededor de los ángulos de la figura, como se muestra en el siguiente diagrama.

Como resultado, el ángulo constante α también se encuentra en FAE y AEF, lo que hace que el triángulo AEF sea similar al triángulo formado por los catetos. Existen también otros triángulos isósceles con un ángulo base β.

El ángulo constante α es de 45° en el Cónsul original, pero la demostración funciona para cualquier ángulo. Al mover solo un pie, el puntero F se mueve en línea recta en diagonal con un ángulo ±α. Esto depende en gran medida de que los enlaces tengan la misma longitud, y si alguna parte difiere en longitud, el movimiento sería curvo y la tabla de multiplicar se distorsionaría.

                    Fuente: https://www.jaapsch.net/mechcalc/consul.htm

 Encontrarás un simulador en https://www.jaapsch.net/mechcalc/consulsim.htm

Algunas de las instrucciones originales podemos verlas en las siguientes imágenes:

Y por último, ¿qué os parecería probar el juego con Consul? Pincha sobre la imagen y llegarás a un simulador, ¿nos cuentas qué te ha parecido?

Fuente: https://en.etudes.ru/models/educated-monkey/